这题的小数据8分,大数据11分,共19分。
在分析解题思路之前,我们先看一下题目中的例子。
假设方案一从来都不买form,那就意味着产生cookie的速率一直都是2个/秒;按照方案二,当买了第一个form之后,速率由2个/秒增加到了6个/秒,买了第n个form之后,速率变成(2+4n)个/秒。
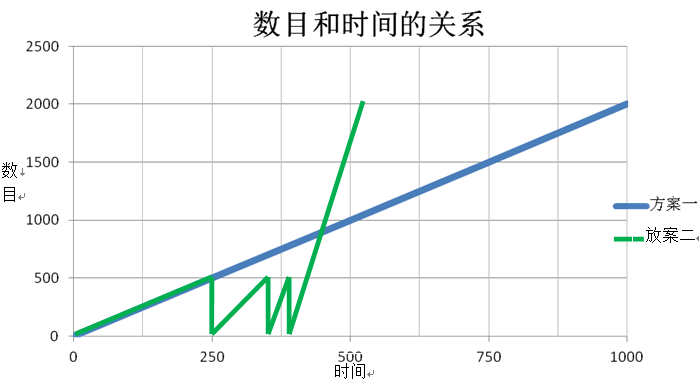
如果以时间为横轴,cookie的数目为纵轴,那么时间和cookie的关系如下图。
从上图中,我们可以看出,第一种方案需要1000秒,第二种方案需要500多秒。
从折现的斜率来看,买的form数目越多,产生cookie的速度越快。但每当买一个form之后,虽然速率增加了,但是cookie的数目马上就减少了。同不买form的那种方案相比,需要一定的时间才能赶上它。
也就是说,我们应当尽量地多买form才能保证多产cookie,但form的数目存在一个临界值,当form的数目多余这个数字时,我们不必买form就能更快地达到要求的cookie数目X。
那这个form数目的临界值是多少呢?
当第一次达到500个cookie时,假设此时的时刻为0,如果不买form,那么再过t秒,cookie数目为 500 + 2t。如买一个form,那么在t时刻的form数目为(2+4)t,也就是6t,那么方案二追上方案一随需的时间是多少呢? 500 + 2t >= 6t,得出t>=125,也就是说,在125秒之前,方案二中cookie的数目小于方案一的数目,这个临界数目是500 + 2t = 750。当产生cookie的数目小于750时,方案一更快,大于750时,方案二更快。
在当前例子中,X的数目为2000,大于750,所以应该采取方案二。
继续产生cookie,当cookie数达到500时,假设我们目前已经有了n个form,如果不买form,再过t秒的cookie数目为500 + (4n+2)t,如果买form,那么再过t秒,cookie数为 (4n+2)t + 4t。我们可以算出,t恒为125,也就是说如果500 + (4n + 2) * 125>=2000,那么应该采用方案一,否则采用方案二。
我们算出n>= 2.5,取整之后form的数目n>=3。
把C,F,X放到公式里,那就是 ( 2 + nF) * C/F >= X – C,然后得到 n的值是 X / C – 1 – 2 / F。那么算上买n次form的时间,加上最后一次的时间 X / ( 2 + n * F ),就是我们所需的结果了。
时间复杂度o(1)。


学习了。