“三门问题”也称为蒙提霍尔问题(Monty Hall problem)、山羊问题,出自美国的电视游戏节目 Let’s Make a Deal。问题名字来自该节目的主持人蒙提 • 霍尔(Monty Hall)。三门问题的前提假设是 :
- 现在有三扇门,只有一扇门后面有汽车,其余两扇门后面都是山羊。
- 汽车事前是随机地被放置于三扇门的其中一扇后面。
回答问题的游戏规则是 :
- 参赛者在三扇门中挑选一扇,但不打开门 ;参赛者在挑选前并不知道此扇门后面是什么。
- 主持人知道每扇门后面是什么。
- 如果参赛者挑了一扇有山羊的门,主持人必须打开另一扇有山羊的门。
- 如果参赛者挑了一扇有汽车的门,主持人在另外两扇有山羊的门中打开一扇门。
问题 :转换选择可以增加参赛者拿到汽车的机会吗?
三门问题的反响
1990 年,《展示杂志》(Parade Magazine)的专栏作家莎凡特(Marilyn vos Savant)曾撰文叙述了三门问题 :
假设你正在参加一个游戏节目,你被要求在三扇门中选择一扇 :其中一扇后面有一辆车,其余两扇后面则是山羊。你最初选择了一道门,假设是一号门,然后知道所有门后面有什么的主持人,开启了另一扇后面有山羊的门,假设是三号门。他然后问你 :“你想选择二号门吗?”你想想 :转换你之前的选择对你得到车有帮助吗?
并给出了她的答案 :
改变初选会更有好处。
没想到这在美国引起了激烈的争议 :人们寄来了数千封抱怨信,很多寄信人是老师或学者 :
- 一位来自佛罗里达大学的博士写道 :“建议以后您专栏里再要回答此类问题时,请 先 看 看 标 准 的 概 率 书 吧。”(May I suggest that you obtain and refer to a standard textbook on probability before you try to answer a question of this type again?)
- 一位来自乔治城大学的读者来信 :“您的回答大错特错 ;我希望这个事件能够唤醒大众对美国数学教育严重危机的重视度。”(You are utterly incorrect about the game show question, and I hope this controversy will call some public attention to the serious national crisis in mathematical education.)
- 另一位大学老师来信 :“至少三位数学研究人员告诉你犯错了,你还是看不见自己的错误。我很震惊!”(I am in shock that after being corrected by at least three mathematicians, you still do not see your mistake.)
可是,莎凡特并没有错!随后她用整整 4 个专栏,数百个新闻故事及在小学生课堂模拟的测验来说服她的读者自己是正确的。“哦,那真是太有趣了。实际上我十分享受这些讨厌的来信!”
初等概率解答
如果选择转换,三门问题可被分解成三种可能的情况 :
- 参赛者之前挑了山羊一号。此时主持人挑山羊二号,转换将赢得汽车。此情况的可能性为 1/3;
- 参赛者之前挑了山羊二号。此时主持人挑山羊一号,转换将赢得汽车。此情况的可能性为 1/3;
- 参赛者之前挑了汽车。“此时主持人挑羊一号,转换将失败 ;或主持人挑羊二号,转换亦将失败。”此情况的可能性为 :1/31/2+1/31/2=1/3.
总结一下 :转换后成功选车的概率是 2/3, 而选不到车的概率是 1/3。
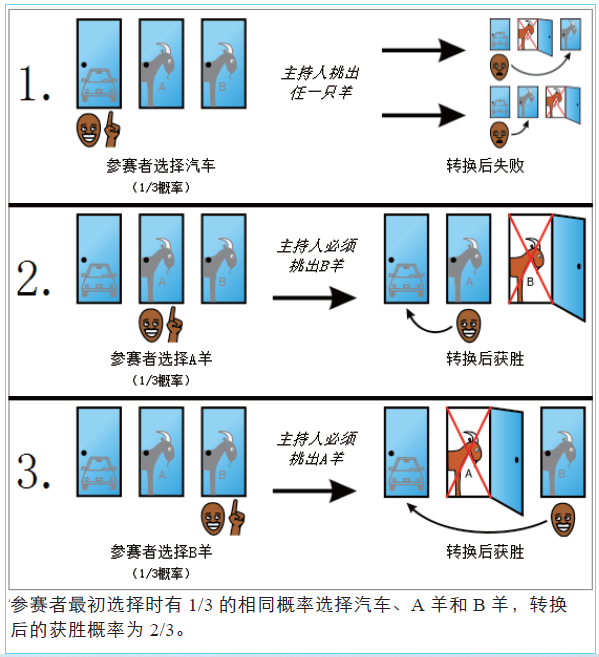
如果用《商业内幕》(Business Inside)2013 年的一篇文章里面的图示方法, 我们可能更清楚地理解这个问题。下面就是相关的三张图。
或者,还有一种更简单的思路。在最开始时,选中车的概率是1/3,选中的羊的概率是2/3。如果参赛者坚持不换,这意味着后续无论主持人开哪扇门都不影响最初的选择。那么,不换门时选中车的概率与初始状态时的概率相同,都是1/3。而换门选中车的概率,则是剩下的2/3。




请你留言